Les tests statistiques sont utilisés à tour de bras dans les sciences les plus diverses: la physique, la biologie, les sciences sociales, etc. Aucune discipline ne semble y échapper. Et pourtant la justification officielle de ces tests ne semble être qu’un tour de passe-passe.
Comme nous l’avons vu dans une précédente publication, les sondages présentaient déjà un biais méconnu découlant d’une erreur de logique grossière puisque détectable par un élève de terminale scientifique en France, donc un lycéen.
Il en est de même dans les tests statistiques parmi lesquels le plus utilisé d’entre eux, le test du khi 2, qui a servi d’illustration dans une publication plus complète sur laquelle nous basons cet article. C’est aussi une erreur de logique qui est à la base de la remise en cause complète des tests que nous pointons ici.
Rappel sur l’usage et le fonctionnement de ces tests
Le mieux est de partir d’un exemple. Imaginons que nous voulions savoir si une molécule donnée, appelons-la « médicament », a un effet sur le taux de globules rouges dans le sang des patients.
Voilà comment il nous est demandé de procéder.
Nous devons sélectionner dans la population humaine deux échantillons. Aux personnes du premier échantillon, nous administrons ce médicament et au second on délivre ce qu’on appelle un placebo, c’est-à-dire une substance que nous savons n’avoir aucune action. Si le médicament est actif, il devra soit augmenter soit baisser le taux de globules rouges dans l’échantillon qui le reçoit et pas dans l’autre. Le problème est de vérifier cette « efficacité ».
Pour cela, il nous faut un outil de mesure. Ici, nous prendrons le taux de globules rouges mesuré par l’analyse de sang adéquate. Ensuite, il nous faut un paramètre qui résumera ces mesures sur l’ensemble de l’échantillon. La moyenne des mesures conviendra parfaitement. Il nous faudra encore comparer les deux moyennes obtenues, donc celles de chaque échantillon. Nous aurons alors ce qu’on appelle un estimateur constitué par le résultat du calcul de cette simple différence. Et c’est là qu’intervient le délicat traitement mathématique.
Pour cela, on va se placer dans l’hypothèse où le médicament ne fonctionne pas. C’est ce qu’on appelle « hypothèse nulle » souvent notée : H0 . Les deux échantillons sont alors simplement deux « tirages » effectués au hasard au sein d’une même population. Et bien évidemment, les deux échantillons ont de grandes chances de ne pas être strictement identiques : nous constatons donc des écarts, on parle de fluctuations d’échantillonnage. Notre estimateur constitué par la différence des deux moyennes va donc être une variable. Pour ne pas manipuler de nombres négatifs, on utilisera la valeur absolue de cette différence ou plus souvent on la mettra au carré. Il est alors tout-à-fait possible de calculer les probabilités d’obtenir telle ou telle valeur pour cet estimateur.
NB: un exposé plus complet et avec le détail des calculs figure dans l’article sur lequel nous nous sommes basés et qui est cité ci-dessus (2).
Ces calculs peuvent alors être résumés graphiquement (figure 1).
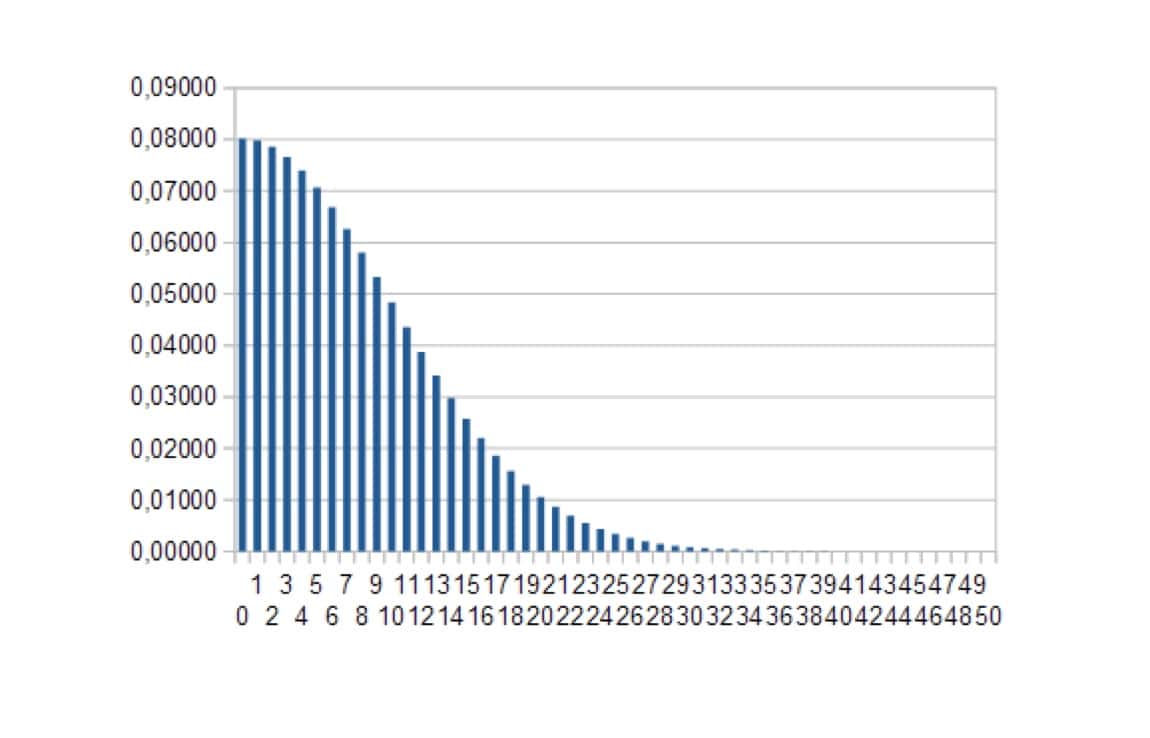
Bien entendu, dans le cas de notre hypothèse nulle (= le médicament ne marche pas) les résultats au voisinage de zéro ont une probabilité plus importante d’être observés que ceux plus éloignés.
Dans notre présent exposé, on ne considérera pas les notions telles que le degré de liberté ou les recommandations sur un minimum de valeurs pour utiliser tel ou tel test puisqu’il ne s’agit pas de remettre en cause un test particulier mais tous les tests qui fonctionnent sur le principe décrit ici.
Il nous est alors demandé de définir un seuil de risque, par exemple 5%. Il s’agit de la probabilité de se tromper.
« vous avez décidé de prendre un risque de 5 % de conclure que les deux variables sont indépendantes alors qu’en réalité elles ne le sont pas »
Il est instamment prescrit de fixer ce taux de risque AVANT de recueillir les données. Il n’est pas de justification formelle mathématique à cette instruction.
« se donner a priori un risque d’erreur »
« Nous décidons du risque que nous sommes disposés à prendre de conclure que les deux variables ne sont pas indépendantes alors qu’elles le sont en réalité. Pour les données de films, nous avions décidé, avant de commencer à recueillir les données, que nous étions prêts à prendre 5 % de risque en déclarant que les deux variables – le Type de Film et l’Achat de Snacks – ne sont pas indépendantes alors qu’elles sont réellement indépendantes. Statistiquement parlant, nous définissons le seuil de significativité α à 0,05. »
« Le test du χ² … permet, partant d’une hypothèse et d’un risque supposé au départ, de rejeter l’hypothèse si la distance entre deux ensembles d’informations est jugée excessive. »
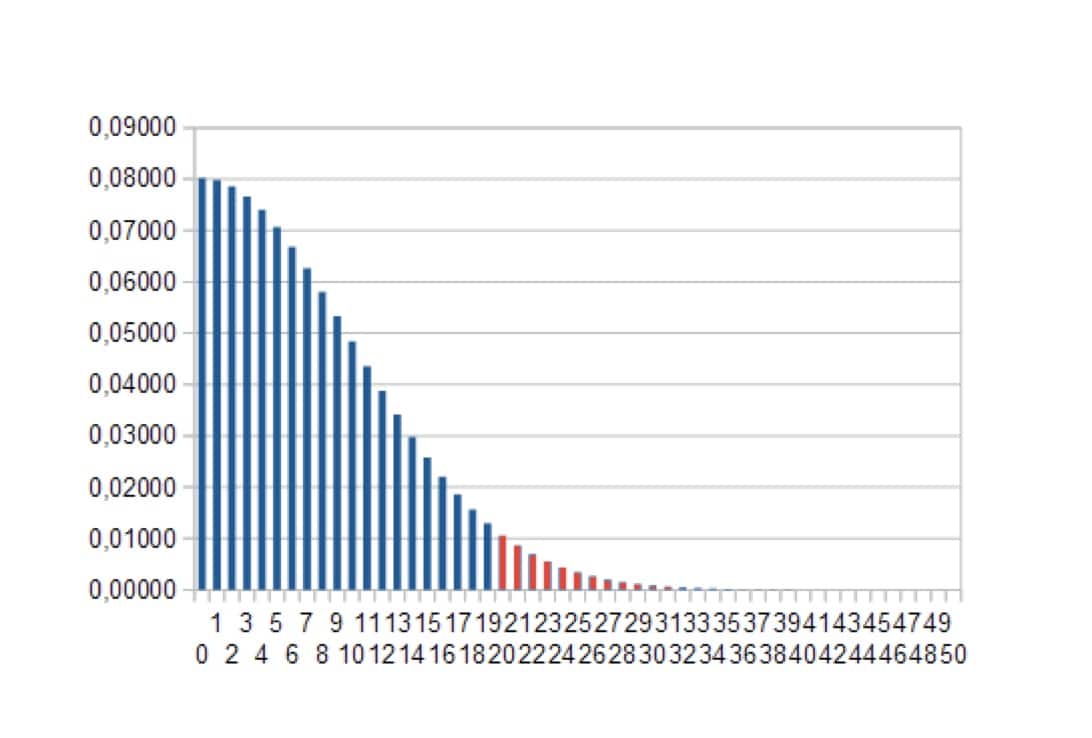
Nous avons colorié en rouge une zone qui représente 5% de probabilité. La zone bleue correspond donc aux 95% restants.
Le raisonnement est le suivant :
Si dans mon expérience, j’ai observé un résultat qui tombe dans les 5%, je peux affirmer, en prenant un risque de 5% de me tromper, que l’hypothèse nulle est fausse puisque celle-ci n’aurait donné un résultat dans cette zone qu’avec une probabilité de 5%. Bien entendu, ayant rejeté l’hypothèse que le médicament ne fonctionne pas, cela signifierait que le médicament est efficace, qu’il influe sur le taux de globules rouges. NB : bien évidemment aussi, si j’ai perdu l’information sur les mesures négatives en considérant la valeur absolue ou en mettant au carré, je ne peux pas conclure sur le sens de cette action : augmentation ou diminution de ce taux d’hématies.
Etablissons d’abord que c’est bien ainsi que sont justifiés ces tests:
« Le risque choisi au départ est celui de donner une réponse fausse lorsque les fluctuations d’échantillonnage sont seules en cause. Le rejet est évidemment une réponse négative dans les tests d’adéquation et d’homogénéité mais il apporte une information positive dans les tests d’indépendance. Pour ceux-ci, il montre le caractère significatif de la différence, ce qui est intéressant en particulier dans les tests de traitement d’une maladie. »
7 – https://fr.wikipedia.org/wiki/Test_du_%CF%87%C2%B2
« Cela signifie que notre khi2 calculé sort de la table par la droite, et a donc une probabilité d’erreur qui est située sous le seuil de 0,01 (soit 1%). Autrement dit, on peut être certains à plus de 99% que nos deux variables ne sont pas indépendantes. »
8 – https://lms.fun-mooc.fr/asset-v1:grenoblealpes+92001+session01+type@asset+block/mod6-cap2.pdf
Certains disent la même chose mais de manière plus prudente en ne parlant pas de risque de se tromper mais de niveau de risque, ce qui est en réalité exactement la même chose :
« Dans la mesure où cette valeur est inférieure au niveau alpha spécifié dans l’onglet Statistiques de test, vous pouvez rejeter l’hypothèse d’indépendance au niveau 0,05. »
Analyse
La situation est donc celle-ci: on prépare deux échantillons et on choisit un seuil de probabilité, ici 5%. Ensuite on demande au calcul mathématique de nous déterminer un seuil, c’est-à-dire la valeur au-delà de laquelle il n’y a que 5% de chances de trouver la valeur de l’estimateur dans l’hypothèse où le médicament ne marche pas. Sur la figure 2, il serait de 20 (axe des abscisses).
Considérons avant l’expérience, tous les cas possibles. Ceux-ci se divisent en deux parties : les cas où le médicament marche et ceux où il ne fonctionne pas. Dans ces deux ensembles de cas possibles, on distingue les cas où l’estimateur va dépasser le seuil déterminé par le calcul probabiliste et ceux où il ne va pas le dépasser. Il y a donc quatre types de cas possibles.
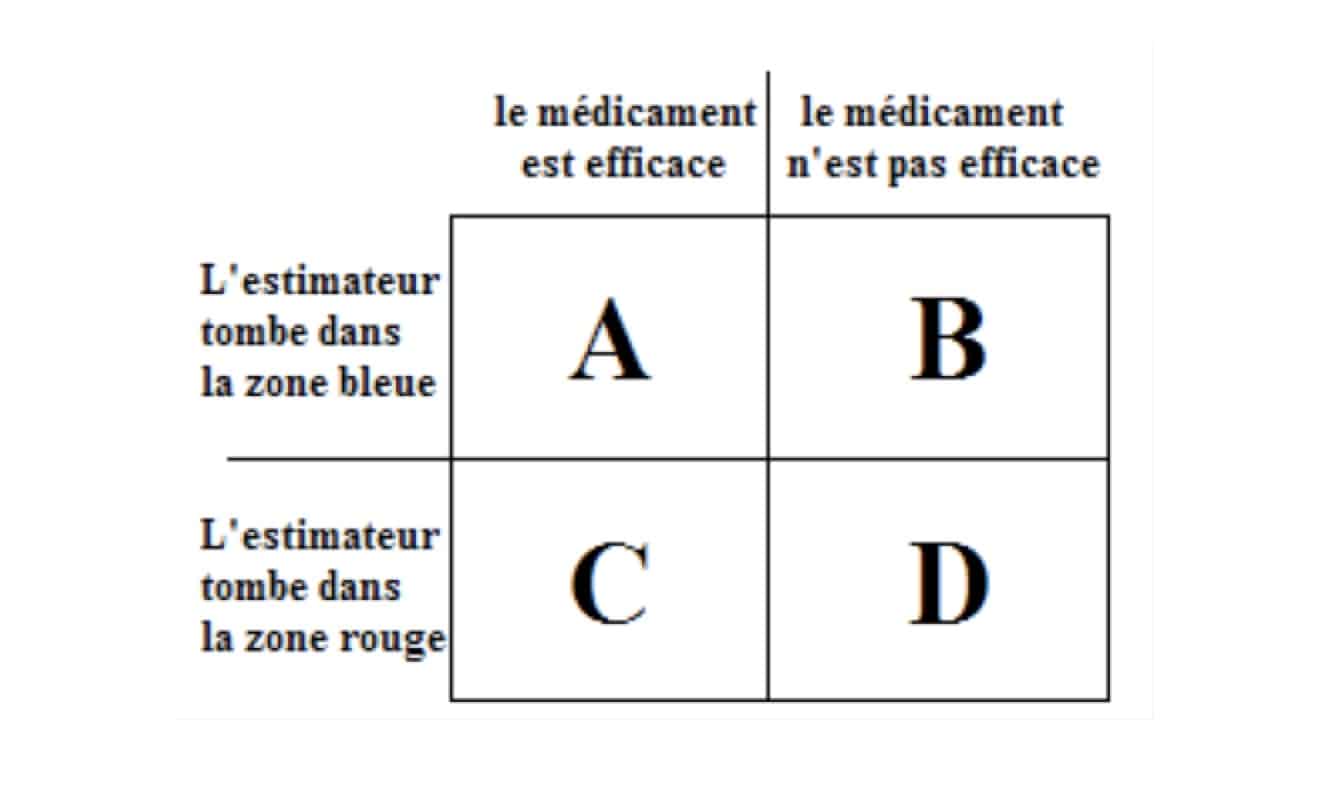
La seule proportion connue est déterminée par le calcul probabiliste : nous savons donc que les cas où l’estimateur dépasse le seuil alors que le médicament n’est pas efficace (D) représente 5% de l’ensemble des cas où le médicament ne marche pas (B+D). Nous ignorons complètement les rapports avec les autres parties.
Nous collectons alors les données ce qui nous permet de connaître la valeur de notre estimateur dans le cadre de notre expérience. Si celle-ci ne dépasse pas le seuil (cas A+B), nous n’affirmons rien, nous ne pouvons que prendre acte que le résultat de notre test n’est pas concluant pour décider si le médicament fonctionne ou pas. En revanche, si notre estimateur dépasse le seuil (cas C+D) alors nous concluons que le médicament marche en pensant prendre un risque 5% de se tromper.
En réalité, ce dernier réside dans les cas où le médicament ne marcherait pas alors que nous affirmons le contraire (les cas D). Les cas possibles après l’expérience ne contiennent plus les cases A et B mais seulement les cases C et D. L’ensemble de cas possibles est donc maintenant C+D.
Or, si nous savons que D représente 5% de B+D, nous ignorons la proportion entre D et C+D. Le risque de se tromper n’est donc absolument pas connu et ne saurait en tous les cas être représenté par les fameux 5% que nous avons utilisés.
Les tests statistiques ne maîtrisent donc pas le risque de se tromper en rejetant l’hypothèse nulle.
Vérification expérimentale :
Considérez des paquets de bonbons. Les bonbons d’un même paquet ont tous la même saveur mais ils peuvent être soit excellents soit très mauvais. Dans les paquets très mauvais, il y en a 5% qui sont emballés en bleu, les autres sont en blanc. Dans les paquets excellents, il y en a plus que 5% emballés en bleu mais on ignore combien. Pour faciliter notre représentation, disons qu’il y en a 10%. Demandez à quelqu’un de choisir un paquet de bonbons. Vous choisissez ensuite un bonbon dans ce paquet sans regarder ni le paquet ni les bonbons à l’intérieur. Si le bonbon est emballé et blanc, vous ne le goûtez pas. S’il est en bleu, vous le goûtez. Si vous pensez que vous avez 5% de chances (établies scientifiquement par un calcul mathématique irréprochable) d’avoir la mauvaise surprise de vous être mis en bouche un bonbon exécrable, vous vous trompez. Imaginons qu’il y ait eu autant de chances d’avoir en mains un paquet excellent qu’un paquet mauvais, vous avez en réalité une chance sur trois d’avoir un bonbon dégoûtant en bouche !
On se rend bien compte que la probabilité d’avoir mis en bouche un bonbon mauvais dépend de la probabilité d’avoir tiré un mauvais paquet et aussi de la proportion de bonbons habillés de bleu dans les bons paquets. Et ici, vous pouvez répéter l’expérience autant que vous voulez, la loi des grands nombres vous confirmera qu’un tiers des bonbons que vous avalez est effectivement très mauvais.
Cette vérification expérimentale vous confirmera la validité de notre analyse et du même coup l’illusion que représentent ces tests statistiques utilisés habituellement et supposés apporter une preuve mathématique de la maîtrise du risque.
Pourquoi a-t-on commis cette erreur ?
En fait, plusieurs points auraient dû interpeller les expérimentateurs. Et donc les amener à se poser des questions. En voici quelques-unes que nous ne développerons pas ici :
1 – Si la zone de 5% représente 5% de se tromper en rejetant l’hypothèse nulle, où sont les 95% restants ?
2 – Si la seule justification du choix de la zone rouge à l’extrême droite de la figure 2 est qu’elle représente 5% de cas, pourquoi ne pas prendre une autre zone ?
3 – Le résultat de l’expérience donne un chiffre précis. La probabilité d’obtenir ce résultat est bien plus faible que celle de toute une zone, pourquoi ne pas réduire le risque en le prenant en compte ?
4 – Les statisticiens insistent sur le choix à priori du risque. Pourquoi ?
Chacune de ces questions (et d’autres encore comme les risques de la seconde espèce…) auraient pu amener ces scientifiques à se rendre compte, chacune par un chemin propre, de ce que nous avons exposé. Cela n’a pas été le cas.
a) Qu’ont donc fait les techniciens des tests ?
Rappelons ici que dans le cas des sondages, il s’agissait d’une erreur de logique. Dans les sondages on avait :
A => (95%) B donc B => (95%) )
L’erreur était alors manifeste.
Ici, on se rend compte que ces techniciens qui valident ces tests font aussi une erreur de logique mais pas la même. Ils se basent sur cet enchaînement logique :
A => B donc nonB => nonA
Ce raisonnement est parfaitement valide en logique pure. Si on sait que, quand A est vrai alors B doit être vrai, il est valide de conclure que, si B n’est pas vrai, alors A ne peut pas l’être non plus. Sauf que ceci n’est vrai qu’avec des probabilités qui seraient égales à 100%. En effet, avec les probabilités des tests, cela donnerait :
A => (95%) B donc nonB => (95%) nonA
Ce qui est simplement faux. Par un tour de passe-passe, le nonB a changé de signification un peu comme dans cet enchaînement logique bien connu:
plus il y a de gruyère, plus il y a de trous
plus il y a de trous, moins il y a de gruyère
donc
plus il y a de gruyère, moins il y a de gruyère
CQFD
Comment une telle erreur a-t-elle été possible ?
Il est toujours possible qu’un jour quelqu’un ait conçu tout cela comme une véritable escroquerie intellectuelle. Théoriquement, oui. Mais celle-ci n’aurait pas tenu aussi longtemps sans d’autres facteurs. Et ceux-ci peuvent à eux seuls expliquer ce qui s’est passé sans avoir besoin d’un esprit machiavélique à l’origine.
L’explication se trouve sans doute plutôt dans le désir immodéré de l’être humain de vouloir contrôler le hasard. Il lui a semblé que le domaine mathématique des probabilités le lui permettait. Et il a ensuite été aveugle à tous les signaux qui étaient pourtant présents pour l’avertir qu’il y avait un problème. On aurait alors à l’œuvre un biais cognitif bien connu, le biais de confirmation.
Comme nous l’avons vu dans l’article consacré aux sondages (1), de nombreuses sciences comme la biologie et surtout les sciences sociales souffraient de la mise en cause permanente que subissaient leurs travaux. Parfois même, certains remettaient en question le statut de science pour ces domaines-là. La venue des tests statistiques a été une bénédiction. Otez-leur ces tests et vous leur coupez un bras sinon les deux.
Mais ils ne sont pas seuls en cause.
Si certaines considérations conduisaient à mettre hors de cause les mathématiciens en ce qui concernait les sondages, elles ne sont plus de mise ici. Il semble au contraire qu’ils aient pris toute leur part dans ce gâchis. Ils pourraient s’être pris au jeu.
Les mathématiciens sont comme tout le monde. Ils ont besoin de reconnaissance. Avant les tests, ils étaient considérés comme des personnes certes brillantes, mais travaillant sur des sujets compliqués et pour la plupart totalement inutiles. Comme reconnaissance sociale, il y a mieux. Avec les tests, tout le monde a besoin d’eux. Les biologistes, les économistes et bien d’autres ont rejoint le club alors limité des physiciens qui étaient jusque-là parmi les rares à vraiment utiliser les mathématiques. L’audience s’est alors élargie à toutes les sciences, en tous les cas à toutes les disciplines qui se prétendent comme telles.
Didier SUARDI et Quentin VALLAD
Annexe : Extrait de « L’espèce la plus intelligente de la planète »

Crédit photo : DR
[cc] Breizh-info.com, 2022, dépêches libres de copie et de diffusion sous réserve de mention et de lien vers la source d’origine














Une réponse à “Les tests statistiques sont-ils une illusion ?”
Alerte ! Ne vous laissez pas berner par ces essais de tests sur des personnes. En réalité, c’est une façon de « recruter » une population prête à l’obéissance sans remettre en question les ordres donnés, écarter celle qui sera résistante à toute subjectivité et, entre les deux tendances, celle susceptible soit d’obéir soit résister à certains ordres. Ce n’est pas du complotisme de dire que CE GENRE DE TESTS A UN EFFET HYPNOTIQUE ! Ne vous rendez pas complices à votre insu de cette manipulation ! N’oubliez pas que sans des complices : forces de l’ordre, vigiles, professions de la bouche, médecins, personnel d’hôpitaux à tous les échelons, lieux de cures, professions de culture ou d’amusement (cinéma, théâtre, ludothèque, blibliothèque, discothèque…), syndicats cgt, cftc, fo.. il n’y aurait pas de Gilets Jaunes ni de manifestants pacifiques maltraités, éborgnés, de personnes sans soins, de personnel soignant, pompiers jetés dans la rue comme de criminels sans indemnités parce que non vaxxinés, personnes en souffrance non soignées… Oui, méfiez-vous, je répète, ne soyez pas complices malgré vous, vous en supporterez les conséquences morales et psychologiques !